Statistical Modeling
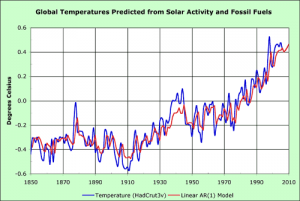
Statistical Modeling is the process by which events of interest are approximated using statistical methods and interpretation. The goal of statistics is to bring uncertainty and complexity into an organized form, allowing it to be quantified.[2] This can be very useful when trying to determine accuracy of collected data, or for approximating the course of an event which has not yet occurred. Though much of statistics can be performed without computers, technology plays a critical role in the ability to generate accurate and useful models for any amount of data. Issues arise when statistical modeling and methods are performed under bias situations or conclusions are drawn incorrectly.
Background
The main goal of statistical modeling is to be able to generalize to a population and expose the relationships between variables of interest. [3] This can be achieved in a number of ways, using a variety of methods.
Generalized Approach
A typical research approach that can be applied to statistical modeling is the scientific method.[4]It begins with a question and the desire to find an answer to the question. This can be formulated by an individual or group of researchers or by a company. It is important to formulate a strong hypothesis, as this will be the basis of the research being conducted. The next step is to decide what sort of data needs to be collected in order to help answer the question and provide enough evidence to accept or reject the hypothesis. The independent and dependent variables should be incorporated into the hypothesis to allow for a relationship between the variables (if any exists) to be exposed. The researcher then goes on to plan out a methodology for data collection. The methodology forms the basis of how the results may turn out, so the researcher focuses a large amount of time planning out an experiment that will be effective while also minimizing errors. The experiment is then executed and the data is tabulated. At this point, data can be quantified and an interpretation can be made.
The Hypothesis
The hypothesis is "an assumption about the population parameter."[5] It is based on background research and formulated accordingly. Usually, it will take the form of a null hypothesis and an alternative hypothesis, where the null implies that there is no significant statistical difference in the data and the alternative supports a significant difference. Statisticians will choose to either reject or accept the null hypothesis based on certain tests, which vary depending on the type of data collected.
Methods of Data Collection
There are two mains forms of data, qualitative and quantitative, and these can drastically affect the type of collection that needs to be done. Qualitative data takes the form of descriptions of what is being sampled, so naturally, the most common way of collecting qualitative data is observation. On the other hand, quantitative data involves numbers and is collected in a more mathematical method. [6]
Here are some common methods of data collection.
| Methods | Description |
|---|---|
| Census | Examines entire population[7] |
| Sample Survey | Examines a fraction of the population [7] |
| Experiment | Controlled method of data collection, based on causal relationships between sample groups[7] |
| Observational Study | Also examines causal relationships, but with less control over sample groups[7] |
These methods all have their uses in specific contexts, and it is up to the researcher to decide which method will be most effective to serve their purpose.
Data Analysis
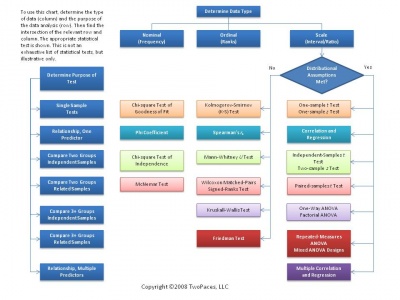
Numerical Analysis
There are many ways of analyzing data numerically, with tests available for practically any type of data, grouping or sample. Some examples include using the mean, t-tests, ANOVA, or linear regression. The table at the right is very helpful for deciding what method of analysis to use. Some of the factors the determine which test is most appropriate include number of groups, paired or unpaired, as well as the specific type of data being analyzed. It is important to use the correct test as using an improper test would lead to incorrect results, and in some cases it is not possible to carry out the calculations. The overall goal of numerical analysis is to describe or compare one or more sets of data. Numerical analysis will typically yield a number which can be used along with values such as degrees of freedom and standard scores to make a conclusion about the hypothesis.
Other advanced forms of data analysis include data mining techniques such as cross validation, where the sample is split into some number of groups, each group taking their turn to test the model that is made from the rest of the data.
Graphical Analysis
Visual representations help depict the sets in a user-friendly manner. They are also used for sharing results of research as well as to support the numerical findings. For categorical variables, bar graphs and pie charts are used. For quantitative data, stem plots, histograms, and box plots are commonly used. [9]
Scatter plots are used to visualize trends and the correlation between two quantitative, continuous variables. When visualizing scatter plot trends, sometimes a line of best fit, or a trend line is included.
Interpreting the Results
Once the researcher has made the necessary calculations, a conclusion can be made about the data set(s). Typically this comes in the form of accepting or rejecting the null hypothesis. In many cases, accepting the null hypothesis means there is no statistically significant difference between the sets of data, while rejecting the null hypothesis means there is a statistically significant difference between the sets of data. At this point, most researchers will include an analysis of their methodology as an explanation of why their experiment may have turned out as it did. Additionally, the researcher will make a statement regarding the certainty or the confidence level of their results. All this information will work towards revealing how accurate the research and results are. This will be the basis for any generalizations that can be made about the population.
Uses
In Medicine
A common use of statistical models is in medicine and they can be applied in many ways. For example, statistical models appear when considering the effectiveness of drug treatments, epidemiology as well as anesthesiology. Additionally, statistics can be used to verify mathematically approximated models such as this model of cardiovascular disease. In this case, the basis for the model is agent based modeling, which is built around programming, however, statistically modeled data could be collected to assess the accuracy of the model. This allows for the creation of a model which can be optimized for efficiency through programming while also being statistically accurate.
Recommender Systems
Recommender Systems are based on algorithms and statistical models which can be very complex. Their goal is to make suggestions to customers based on past search history or past purchased items. They can be found on retail sites like Amazon, music sites like Spotify, or even WebMD for determining what illness a person may be experiencing. These systems typically act in two ways: predictive algorithms, and learning algorithms.[10] Both these principles can be programmed based on statistical models, and the results of the algorithms can be confirmed using statistical models.
Stochastics
Stochastics is the use of stastical analysis wih a random variable, therefore the analized material can not be predicted percisely. Stochastics has a wide range of uses including in the natural sciences of physics and biology, in computer science, and even in the buisness world. Infact manufacturing and the insurannce insurance industry both use stochastics regullarly.[11]
Politics
In the political and public policy realm, statistics and numbers are used to evaluate the economy, Congressional and Presidential approval, election outcomes, and demographics. Various predictive models are used to determine the winner of an election, and to evaluate Presidential approval over the course of Presidency. When evaluating the economy, statistics are used to look at correlations and trends in spending, saving, and potential causes of an economic depression.
Ethical Concerns
Statistical modeling yields a representation of an event of interest, so by its nature, there are points in the modeling process that can be improperly implemented, or misused, with or without intention. This forms the basis of a widespread debate regarding the accuracy of statistical models and the extent to which they can trusted and generalized to a population.[2]
Bias
In any process of collecting data, there can be bias present. This bias can come from either the researcher or from the data itself. Sampling bias occurs when the researcher selectively samples certain data, which can reflect their personal biases from beliefs or from a desire to yield a certain result in the data. Additionally, bias may be present in the sample itself, from cases of non-response and self selection.[2] For example, if random interviews were being conducted on a street, some people may avoid the interviewer and some may seek out being interviewed, and this can drastically influence the beliefs reflected by the interviewee. This makes it imperative for the researcher to follow a strict code of ethics in order to avoid any of the aforementioned biases. These codes include accurate reporting of data and information and assurance of data quality (for example, using a genuine random sample). [12]
High bias in results comes at the cost of low variability, in a phenomenon known as the Bias-Variance Tradeoff. In statistics, the ideal results should have an optimal amount of both bias and variability in data, keeping both at a minimum simultaneously. Skewness of one being higher at the cost of another can lead to ethical issues when interpreting data.
Misleading Statistics
In addition to biases that may be present in a statistical model, statistics can be altered and used inappropriately to support an argument that otherwise may not be supported by the model. Statistical models may also be misleading in the way they are represented, whether intentionally or not. In this case, a statistical model may be accurate but the wording or depiction of the data may not afford for an explanation to be apparent.[13] This is one of the many reasons that peer review has been necessary when it comes to any form of professional statistical work. It allows for areas of ambiguity to be clarified, while also allowing others to determine if there has been any intentional misrepresentation of the data.
Simpson's paradox is a phenomenon in statistics that shows trends and numbers moving in the opposite direction when pooled properly over when they are shown in aggregate. Simpson's paradox can be a way to show misleading statistics by leaving out information, and not talking about what the data doesn't show.
In the Media
One notable ethical issue regarding statistical models was the case of Target's recommender systems predicting a girl was pregnant before her father knew. The situation arose when a teenage girl shopped at Target for pregnancy related items, after which Target began sending the girl pregnancy related coupons. The father noticed this occurring and was very angry with Target for sending such materials to his daughter, until he realized that she was indeed pregnant. This raises a very serious privacy issue regarding the appropriate use of recommender systems. This situation made it very apparent that recommender systems can, in some cases, reveal personal information so parties that should not be exposed to this information.
Another case occurred when Susan G. Komen for the Cure published research regarding breast cancer treatment and diagnosis. The problem that arose was in Komen's rallying for women to be regularly screened for breast cancer. They stated the benefits of screening but failed to mention the rate of misdiagnosis, and the resulting psychological issues and potential unnecessary treatment for the woman in question. This is a case where their statistics regarding the early diagnosis survival rates did not accurately represent anomalies that regularly occur in the medical system. [14] Similarly, this has occurred when the statistics relevant to new drugs are found to be misleading, even by educated doctors.
In 1973, UC Berkeley was sued for sex discrimination against women, where statistics showed favor of men. When looking at the data more closely, and separating admissions by department or "properly pooling the data", results showed a slight favor towards women. [15]
See Also
Data Mining Data Aggregation Online
External Links
References
- ↑ Cobb, Loren. The Causes of Global Warming: A Graphical Approach. 2007. Photograph. n.p. Web. 9 Oct 2012. [1].
- ↑ 2.0 2.1 2.2 Kaplan, Daniel. Statistical Modeling: A Fresh Approach. 2nd ed. Saint Paul: Project Mosaic, 2012. vii. Print.
- ↑ “New View of Statistics: What Is a Model?” Sports Sci, Will G Hopkins, 2000, www.sportsci.org/resource/stats/models.html.
- ↑ Guch, Ian. “Scientific Method.” Misterguch.brinkster.net, 20 Aug. 2014, misterguch.brinkster.net/scientificmethod.html.
- ↑ “Hypothesis Tests.” Stat Trek, 2018, stattrek.com/hypothesis-test/hypothesis-testing.aspx.
- ↑ “Qualitative vs. Quantitative.” Regentsprep.org, www.regentsprep.org/Regents/math/ALGEBRA/AD1/qualquant.htm.
- ↑ 7.0 7.1 7.2 7.3 “Data Collection Methods.” Stat Trek, 2018, stattrek.com/statistics/data-collection-methods.aspx.
- ↑ “Statistics Help.” Twopaces.com, twopaces.com/stats_help.html.
- ↑ “Statistical Graphs, Charts and Plots.” Statistical Consulting Program, pages.csam.montclair.edu/~mcdougal/SCP/statistical_graphs1.htm.
- ↑ Agarwal, Deepak K., and Bee-Chung Chen. “Machine Learning for Large Scale Recommender Systems.” Statistical Methods for Recommender Systems, pages.cs.wisc.edu/~beechung/icml11-tutorial/.
- ↑ “Stochastic.” Oxford Dictionaries | English, Oxford Dictionaries, en.oxforddictionaries.com/definition/Stochastic/.
- ↑ Forum Guide to Data Ethics. NFES 2010-801. [S.l.]: Distributed by ERIC Clearinghouse, 2010.
- ↑ “Misleading Statistics.” Responsible Thinking, www.truthpizza.org/logic/stats.htm.
- ↑ "Susan G. Komen for the Cure Misleading Statistics" http://www.krdo.com/news/Susan-G-Komen-for-the-cure-misleading-statistics/-/417220/15968152/-/8vijbpz/-/index.html
- ↑ Bickel, P. J., et al. “Sex Bias in Graduate Admissions: Data from Berkeley.” Science, vol. 187, no. 4175, 7 Feb. 1975, pp. 398–404., doi:10.1126/science.187.4175.398. http://www.unc.edu/~nielsen/soci708/cdocs/Berkeley_admissions_bias.pdf